「题解」HNOI2003 激光炸弹

基本思路

基本的二维前缀和，把从（0,0）到任何一个点围成的矩形中所有的价值计算出来，然后再通过容斥原理算出所有可能正方形中的价值之和。

如果把初始的地图存入A数组，那么它的二位前缀和S就是：

$S[i][j]=\sum_{x=1}^{i} \sum_{y=1}^{j} A[x][y] $

根据容斥原理，有：

$S[i][j] = s[i-1][j]+s[i][j-1]+A[i][j]-S[i-1][j-1]$

这样，就可以利用上述递推式推出S数组。

同时，对于任意一个边长为R，最靠近原点的顶点为$(x, y)$的正方形，其内部所有点的价值之和为：

$S[x+R][y+R]-S[x+R][y]-S[x][y+R]+S[x][y]$

这样，就可以以$O(n^2)$的时间复杂度解题。

我踩过的坑

1. 这题有125MB的空间限制，根据上述递推式，只需要一个数组就可以完成，开两个范围为5000的二位数组貌似过不了。。

2. 数据规模约定中，n最大可以到$10^4$，然而并没有那么大的地图，相当于“全图轰炸”，此时效果与$n=5*10^3$效果相同，可以直接替换。数组开到$10^4$的话会爆空间的。

3. 数组稍微开大一点点。

4. 最重要的一点，数据要从$(1,1)$开始存，也就是说，边界应该为0,这样才能保证边界的数可以被正确计算

我一开始没有注意第3点，之后在洛谷得了90分，被这样一个数据卡住了：

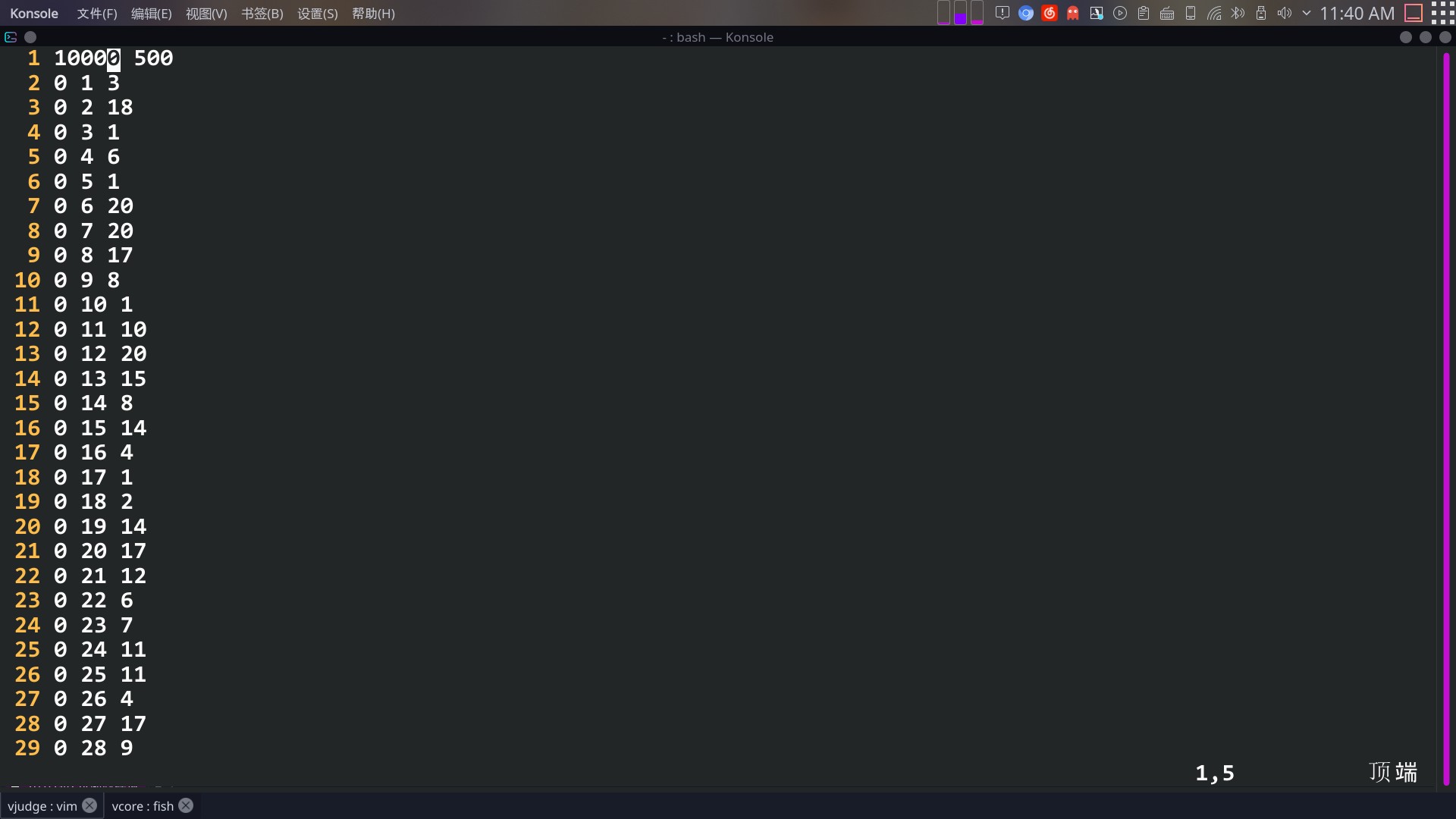
可以看到，全是第0列的点。。

之后自己造了一个数据，成功发现了这个问题：

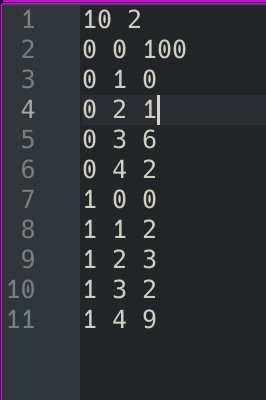
代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
using namespace std;

const int MAX=5002;
int s[MAX+5][MAX+5], n, r, summ, maxx, x, y, w;
int xmax, ymax;

int main(){
//	freopen("data.in", "r", stdin);
	scanf("%d %d", &n, &r);
	if(r>5000) r=5000;
	for(int i=0; i<n; i++){
		scanf("%d %d %d", &x, &y, &w);
//		xmax = xmax>x?xmax:x;
//		ymax = ymax>y?ymax:y;
		s[x+1][y+1] += w;
	}
/*	for(int i=1; i<=MAX+2; i++){
		s[i][0] += s[i-1][0];
	}
	for(int i=1; i<=MAX+2; i++){
		s[0][i] += s[0][i-1];
	}*/
	for(int i=1; i<=MAX+2; i++){
		for(int j=1; j<=MAX+2; j++){
			s[i][j] += s[i-1][j]+s[i][j-1]-s[i-1][j-1];
		}
	}
	for(int i=0; i<=MAX-r; i++){
		for(int j=0; j<=MAX-r; j++){
			summ = s[i+r][j+r]-s[i+r][j]-s[i][j+r]+s[i][j];
			maxx = maxx>summ?maxx:summ;
		}
	}
	maxx = maxx>s[r][r]?maxx:s[r][r];
	
	printf("%d", maxx);

	return 0;
}